In This Issue
Modular Synthesis for Beginners – Oscillators, Part 2: Additive Synthesis
Everything just adds up when you understand how harmonics work.
As musicians, we work with sound. Sure, wearing the right pair of pants in the photo shoot is important, but as Moog Music said in an ad for the Minimoog back in the early 1980s, “When you have the sound, you don’t have to talk about it so much.”
But really, what’s in a sound? In theory, any periodic (repeating) sound can be analyzed as a collection of sine waves, each with its own frequency, amplitude (loudness), and phase. This is a bit of a mathematical trick. A true sine wave is an abstract thing in trigonometry, and unless you own a synthesizer, you’re not likely ever to hear one in the real world. In spite of that, the trick turns out to be incredibly useful.
The technical term for sounds that never repeat is noise. The sounds of wind and surf are prime examples of noise.
If you’d like to know more about the theory, you can search online to learn about Fourier analysis. This mathematical theory is named after Jean-Baptiste Fourier. Hermann von Helmholtz, who built a physical resonator that allowed him to isolate the sine wave resonances in physical sounds in the 19th century, also contributed to the theory.

It All Adds Up
This idea—that complex sounds can be analyzed as consisting of stacks of sine waves at different frequencies and amplitudes—is important in synthesizer sound design, because it allows us to build up complex and interesting sounds by mixing sine waves with one another. This technique is called additive synthesis.
In many physical instruments, the frequencies of the sine waves will be simple multiples of one another—or close to them, depending on the instrument’s physical imperfections. For example, if a guitar string is vibrating at 100Hz (100 cycles per second), the complex tone of the string will also include vibrations at 200Hz, 300Hz, 400Hz, and so on. These vibrations are called overtones or harmonics, and the 100Hz vibration is called the fundamental. There’s no need to get into the linguistic distinction between these terms; instead, we’ll use the more general term partials to refer to all of them. In any complex periodic sound, the sine wave components are called partials.
Any sine wave component of a complex sound is a partial, whether or not its frequency is related in a simple mathematical way to the frequency of any other partial. A bell produces partials that are not whole-number multiples of the fundamental. Tones of this type are referred to as clangorous, because in some sense, they clang like a bell.
The Hammond drawbar organ was an early example of an additive synthesizer. It produced tones mechanically rather than electronically. Digitally producing a bunch of sine waves and then mixing them tends to be a bit intensive in terms of computer power, so it wasn’t practical to do additive synthesis in real time on the first generation of digital synthesizers. Today, however, we can do additive synthesis quite easily (and without having to lug around a 200-pound Hammond organ).
Producing realistic sounds—of a violin, saxophone, or guitar, for instance—using additive synthesis tends to be a finicky process, for a couple of reasons. First, you have to adjust the amplitude and pitch envelopes of quite a lot of partials. You probably won’t find the information on how to do that in a convenient recipe book, though various bits of obscure information can be found online using a search engine. Second, most real-world sounds include a bit of noise. The rasp of the bow across a violin’s strings and the breath sounds in a sax tone are a form of noise. Noise can’t be produced using additive synthesis, because noise is, by definition, not periodic, so Fourier analysis can’t make heads nor tails of it.
Additive synthesis is a much better resource for making sounds that don’t try to be realistic. That’s what we’ll look at in this month’s video. Additive is also important for theoretical reasons. When you start working with filters, a topic we’ll get to in a couple of months, you’ll need to understand that filters work by reducing the loudness of some of the partials within a composite tone.
Hands On
VCV Rack boasts several additive oscillators, including Bogaudio Additator, Blamsoft XFX Wave, Squinky Labs Chebychev, Nysthi Phasor, and Autinn Jette. Alternatively, you could experiment with additive synthesis by patching a bunch of separate sine wave oscillators into a mixer, but getting anything that sounds decent from a bank of separate oscillators would be a thankless process.
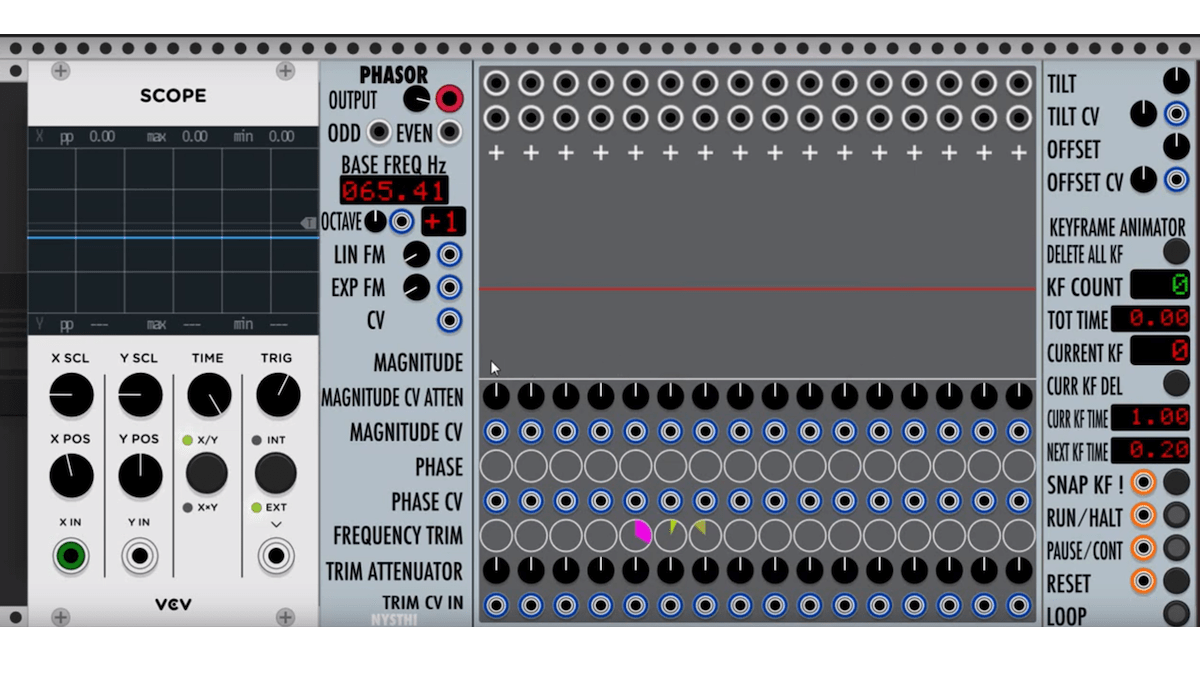
For this month’s tutorial patch, we’ll use Nysthi Phasor. It has a good visual display and some powerful features. The best way to develop an understanding of Phasor may be to watch the video. We won’t have space to delve into this module’s more advanced capabilities, but here are a few basics to get you up and running:
1) The right-click menu within the gray area is different from the normal right-click menu (and more useful).
2) I generally switch off Show Phasor, Show Path, and Show Wave in the right-click menu. This reduces the CPU load slightly and makes for a cleaner display. But leaving them switched on may be educational.
3) You can adjust the amplitudes of the 16 partials with the bar graph elements.
4) You can adjust the frequencies of individual partials up or down with the Frequency Trim knobs. These don’t look like knobs; they look like empty circles. (Also, they don’t respond to the normal VCV method of being centered by double-clicking. To re-center the frequencies, use the right-click menu.)
5) You can use the rows of input jacks below the bar graph for modulating individual partials. LFOs and envelope generators are good sources for these modulation inputs. You can produce a wide variety of colorful sounds by modulating the amplitudes of various partials.
One thing to bear in mind as you watch the video is that the compression codec used by my video capture software (Camtasia Studio) does not handle sine waves well. It garbles them. In order to appreciate what’s going on in the video, you’ll probably want to install VCV Rack, if you haven’t done so already, and then mess with the downloadable patch files.
Links to Download: Additive_A.vcv, Additive_B.vcv, Additive_C.vcv, and Additive_D.vcv
The Sum Total
As you’ll see in the video, envelope generators and LFOs are good sources of modulation signals for controlling the amplitudes of partials in additive synthesis. Even at its most complex, though, additive synthesis tends to sound rather clean and pure, probably too clean and pure for aggressive pop music. In the next couple of months, we’ll look at ways to produce rich expressive tones using oscillators.

















